Digitale signalen en quantisatie

Wij hebben elders gezien dat digitale audio erop neerkomt dat men een continu signaal s(t) beperkt tot een reeks s(n) waarbij het volggetal n verwijst naar de opnametijdsstippen tn = n.Dt en waarbij de periode Dt oordeelkundig gekozen wordt. Dit laatste wil zeggen dat als men het ganse spectrum wil herconstrueren vanuit deze samples dat de samplingfrequentie fs minstens het dubbele moet zijn van de hoogste frequentie - componenten in het spectrum van het signaal. Maar dat is niet het volledige verhaal over digitale audio . Ook de exacte samplewaarden worden niet weerhouden maar slechts tot één van de mogelijke 2^b waarden wanneer een b-bits sampler wordt gebruikt. Deze benadering van de waarde van het signaal wordt quantisatie genoemd . De quantisatiestap Q  is niets anders dan het kleinste verschil tussen twee gequantiseerde signaalwaarden.

De informatiedensiteit die wordt geëist is dus (b*fs)  bits/seconde! Een belangrijke vraag die zich stelt is de volgende : is deze datadensiteit steeds vereist om  een acceptabel hoorbare reproductie te garanderen van het oorspronkelijk signaal. Essentieel  komt het hier op neer dat een acceptabele wiskundige benadering van een signaal en een acceptale auditieve benadering van een signaal twee verschillende zaken zijn !

De quantisatie afwijking van het signaal kan geresumeerd worden door  te stellen

s_q(n) = s(n) + q(n)

waarbij het linkerlid dus de waarde van het signaal voorstelt dat effectief zal gebruikt en gestockeerd worden , q(n) stelt dan de al dan niet hoorbare quantisatieafwijking voor met de eigenlijke signaalwaarde.Deze afwijking stelt dus infeite een soort  ruis voor die men quantisatieruis noemt. Hoe kleiner het aantal bits hoe groter   deze ruis wordt . Belangrijk hierbij is de afweging van de hoeveelheid energie er steekt in deze quantisatieruis tot de volledige hoeveelheid energie in het signaal. Deze belangrijke grootheid wordt de Signaal/Ruis verhouding genaamd en gedefinieerd als:

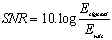
Hierin is Esignaal de energie in het signaal en Eruis de energie in de quantisatieruis.

Wanneer de quantisatieafwijkingen en de signaalwaarden optreden  volgens een uniforme verdeling dan kunnen deze twee energies berekend worden en de invloed van het aantal bits op de grootheid SNR vastgesteld worden. Bij een uniforme ruisverdeling zal de energie in de ruis gelijk zijn aan:

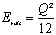
Daarentegen is de gemiddelde enrgie in een signaal waar alle signaaalwaarden met gelijke waarschijnlijkheid kunnen optreden gegeven door:

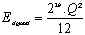
of in decibels geeft dit voor de quantisatieruis:

en voor het signaal geeft

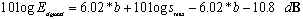
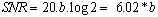
Wil men dus een dynamisch bereik halen van 75 dB ( hi-fi) , dan moet men minstens te maken  hebben met 12 bits quantisatie en dat voor een kwaliteits speech codering aan 8 kHz er dus een stroom van 12*8000 = 96000 bps nodig  zal zijn !!

Quantisatieschema's kunnen opgedeeld worden als zijnde uniform of niet-uniform, vast ( in de tijd) of adaptief (niet vast in de tijd). De keuze hiervan hangt gedeeltelijk af van welk type signaal men beschouwt.

Puls Code Modulation ( P.C.M )

Uniforme quantisatie

De eenvoudigste manier van quantisering en vervolgens van (binaire) codering van deze waarden bestaat uit het gebruik van een lineaire quantisatie ,dus een uniforme vaste quantisatiestap Q , en het toekennen van een  binaire waarde aan de gequantiseerde signaalwaarde. Om historische redenen werd dit PCM genaamd. Dit is de simpelste ,vlugste  en meest directe manier van codering en infeite de enige manier die een normale sampler toelaat.

Het moet echter duidelijk zijn dat de stille passages in een opname dan ook gevoelig zijn aan  de quantisatieruis. Deze vorm van codering doet het vooral derhalve goed voor signalen met een uniforme distributie van de signaalwaarden. Spraak is echter niet zo iets .Onze spraak vertoont vele stille passages tussen klankovergangen .Dit is zeker het geval om en bij de plofklanken . Deze passages zijn echter essentieel voor de verstaanbaarheid daar zij de phonemen , klankeenheden afbakenen en dus iets te maken hebben met ons alfabet. Met lineaire quantisatie zouden deze een kleine S/R hebben wat wij moeten trachten te voorkomen.

figuur: 'pop' en 'po'  in 8000Hz en 16 bits

Uniforme quantisatie is dus hier niet goed en beter is een niet lineaire (niet-uniforme ) vaste quantisatie te gebruiken.

Niet- uniforme quantisatie , companding-PCM

Voor spraak is het dus gewenst niet-lineaire quantisatie toe te passen . Deze operatie wordt companding ( compressie-expansie)  genaamd . De operator , die  wordt toegepast vóór de sampling eigenlijk gebeurt , staat bekend als  een compressor . De omgekeerde operatie met als doel het signaal te restitueren is de expander .

De meest bekende zijn de logaritmische companders waarvan de meest gebruikte types zijn de m-en A companders die wij elders uitvoerig behandelen .Een voorbeeld

Adaptieve PCM ( ADPCM)

In de voorgaande quantisaties wordt dezelfde quantisatiecodering op alle samplepunten toegepast . Spraak en nog  andere signalen hebben echter een sterk veranderlijke envelope (omhullende aan de energie ) en het zou dus voordelig zijn de quantisatie aan te passen aan de grootte van de energie. Het basisidee van adaptieve quantisatie bestaat erin de quantisatiestap te variëren  zodat een match met de variantie van het signaal wordt bekomen.

Adaptieve quantisatie coders zijn oftewel feedforward of feedbackwards .

         Q(k+1) =Q(k).V(k+1)

met V zijnde de geschatte waarde van de  variantie  over een venster met een breedte van M punten :

          Q(k+1)= M(k).Q(k)

M(k) hangt dus af van de voorgaande quantisatie-outputs. In voorgaande betrekking wordt een scalair product uitgevoerd . De waarden van deze adaptieve operator wordt meestal meegegeven in een opzoektabel

De standaard ADPCM coder leest een 8-bit  PCM signaal van 64000 bits/s in .Door toepassing van een adaptieve voorspelling en toepassing van een 4-bit adaptieve quantiser M (deze heeft dus 16 waarden) kan de sampledensiteit herleid worden tot 32000 bps . De adaptieve decoder doet juist het tegenovergestelde en herstelt de 64000 bps.Wij beluisteren zo een ADPCM signaal.