Gegevens
Bij het invallen op de wand ontstaan een gereflecteerde golf  pr en een doorgelaten golf  pd.  De totale druk aan de zendzijde is dan: p1 = pi + pr.   De druk aan de ontvangzijde is p2 = pd.   v is de snelheid van de wand volgens de invalsrichting.

massawet2.gif (2279 bytes)

Vergelijkingen

Dynamisch evenwicht

 $p_1 - p_2 = m''\frac{dv}{dt}$        (1)
Harmonisch schrijven we dit als: $\underline p_1 - \underline p_2 = \underline T \underline v$ met T = jw m" (= complexe scheidingswandweerstand).

Klik hier om een popup met meer info te openen

Verder weten we dat voor een vlakke golf geldt:  p2 = Z v  (met Z = rc). (Bewijs dit)
Vergelijking (1) wordt dus: $p_1 = \underline v (Z + \underline T)$

Continuïteitsvergelijking

 $\underline v_1 = \underline v$        (2)
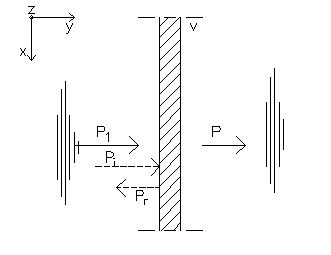
v1 is de resulterende deeltjessnelheid aan de invalszijde.

Randvoorwaarden

 De randvoorwaarden leveren twee bijkomende vergelijkingen op:

$\underline v_1 = \underline v_i + \underline v_r \ \ en \ \ \underline p_1 = \underline p_i + \underline p_r$      of
$Z \underline v_1 = Z \underline v_i + Z \underline v_r \ \ en \ \ \underline p_1 = Z \underline v_i - Z\underline v_r$
De som van deze beide vergelijkingen is dan: $\underline p_1 + Z\underline v_1 = 2Z \underline v_i$        (3)
Uit vergelijkingen (1) en (2), gecombineerd met de randvoorwaarden (3) volgt: $\frac {\underline v_i}{\underline v} = 1 + \frac{\underline T}{2Z}$
De geluidisolatie bepalen we door de verhouding van de intensiteit van de invallende golf t.o.v. de doorgelaten golf:

$R = 10\ \log \frac{1}{\tau} = 10\ \log \frac{I_i}{I_d} = 10\ \log (\frac{V_i}{V})^2 = 20\ \log \frac{\underline v_i}{\underline v}$
R wordt dan: $R = 10\ \log \{1 + [\frac{\omega m''}{2Z}]^2\}$.
Vereenvoudiging van de bovenstaande vergelijking levert de massawet op: $R_0 = 20\ \log \frac{\omega m''}{2Z}$.

© Laboratorium Bouwfysica, K.U.Leuven