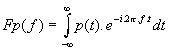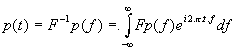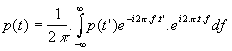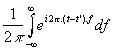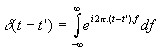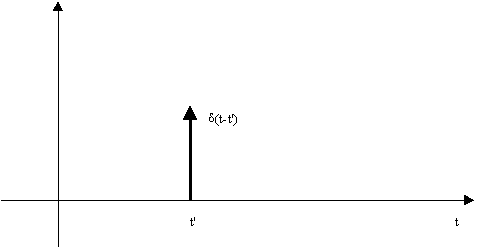De Fouriergetransformeerde van een oneindig lang signaal
Veronderstel dat een signaal integreerbaar is over de ganse tijdas . Dit veronderstelt ondermeer dat de signalen moeten dempen in het oneindige . Voor deze signalen kan men een Fouriergetransformeerde (FT) definiŽren als volgt:
Lees dit als ' de Fouriergetransformeerde van p(t) met frequentie f is ....' . Natuurlijk een functie kan men altijd transformeren naar gelijk wat , de vraag is echter of dat men door inverse transformatie terug kan naar de oorspronkelijke functie , en bovendien stelt zich de vraag of de transformatie een meerwaarde aan informatie over het signaal geeft ,slechts dan worden deze bewerkingen zinvol. In het vernoemde geval bestaat de invertering , nl :
Op analoge wijze als bij Fourierexpansies wordt Fp(f) de Fouriergetransformeerde (Fourierspectrum) van p(t) genoemd en is dus nu continue, de variabele f is wel degelijk een continue frequentievariabele.
Merk de grote symmetrie op tussen de tijdsruimte en de spectrumruimte.Voor de formules maakt het niet uit ofdat wij met een tijdssignaal bezig zijn of met een spectrumsignaal !
Alhoewel Fourierreeksen en transformaties los van elkaar zijn gedefinieerd is het wel zo dat voor periodische signalen de FT die strikt gesproken niet bestaat ,daar deze functies bij definitie niet integreerbaar zijn over de tijdsas ,toch mits enig trucwerk en het gebruik van veralgemeende functies, terug te brengen is tot een acceptabele FE!! Inderdaad de voorgaande invertering veronderstelt reeds het gebruik van een ongewoon signaal nl
veronderstelt dat
niets anders doet dan de variabele t' in p(t) te substitueren door t ! Deze veralgemeende functie wordt de Dirac Delta functie genoemd en als volgt genoteerd:
Hoe ziet deze functie er ongeveer uit ? Daarvoor berekenen wij de vorige integraal van -F tot +F (slechts achteraf laten wij F naar oneindig gaan ), wij bekomen :
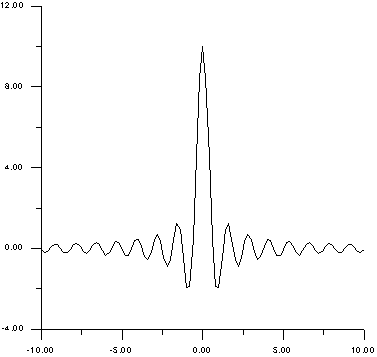
Voor elke waarde van t' verschillend van t is deze functie nul met uitzondering als t = t' dan is zij oneindig. Een goede weergave vindt u in de volgende figuur , x = (t-t').
figuur 1 de sincfunctie
De limiet waarde van deze functie wordt grafisch voorgesteld als:
figuur 2 : de Dirac-Delta functie
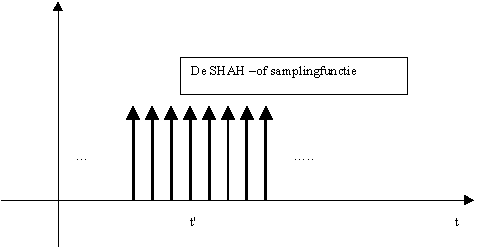
Een veralgemeende functie die hier sterk mee verband houdt en ons vele goede diensten gaat bewijzen om digitale signalen te beschrijven is de Shah - of Samplingfunctie voorgesteld door
De grafische voorstelling ziet er uit alsvolgt:
figuur 3 : de Shahfunctie
Dank zij deze veralgemeende functies kunnen wij zelfs voor alle periodische functies ( of eindige functies met perfecte looping) een FT definiŽren. Immers deze functies f(t) hebben dus uiteraard een FR van de vorm:
als wij deze Fourier transformeren bekomen wij als acceptabel spectrum:
We trekken hieruit de volgende belangrijke lessen:
| Het FT van een periodisch signaal met periode T kan inderdaad omschreven worden en bestaat uit discrete waarden op de frequenties |
deze herkennen wij als het reeds bekende harmonisch spectrum met waarden Zm .
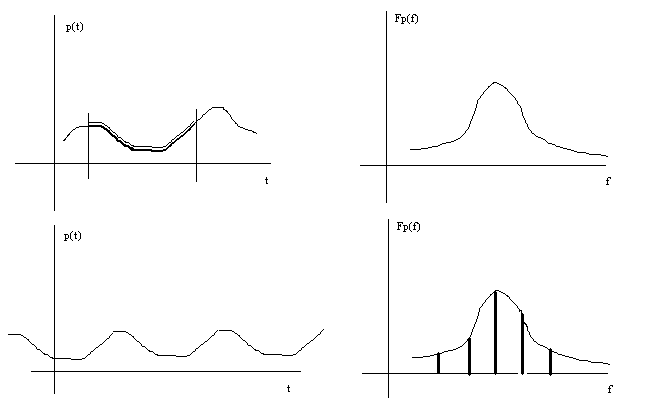
| Een andere interpretatie van voorgaande uitdrukkingen is de volgende.Wanneer wij een continu spectrum bemonsteren met een periode 1/T dan selecteren wij uit het oorspronkelijke signaal een tijdspanne T dat wij vervolgens periodisch voortzetten. | |
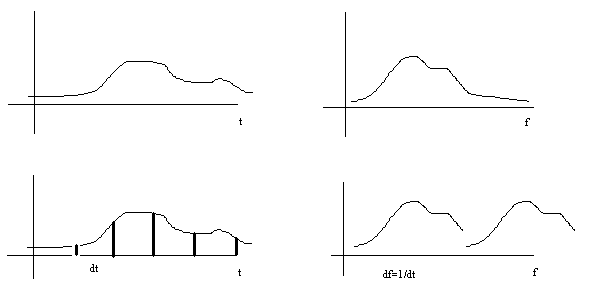
| Gezien de duidelijke dualiteit tussen de variabelen t en f ( de formules verslikken zich immers in deze vermenging) geldt ook het omgekeerde.Wanneer wij een gegeven signaal met een bijbehorend spectrum samplen met periode T dan selecteren wij uit het spectrum een bandbreedte Df = 1/T en maken dit spectrum periodisch met periode 1/T. Immers zij gegeven een signaal p(t) met een FT nl Fp(f) en bemonsteren wij het signaal met een herhalingsperiode Dt dan kunnen wij dit nieuwe signaal schrijven als |
en de FT hiervan is dan triviaal:
welke wij interpreteren als een periodisch-harmonisch spectrum met als harmonischen n/T .
| Deze beschouwingen zullen ons toelaten digitale signalen te beschouwen tesamen met hun spectrum. |
| Misschien is een grafische interpretatie van deze besluiten veel duidelijker en deze geven wij hieronder. |
figuur 4: sampling van een spectrum betekent dat een eindig stuk signaal wordt geselecteerd en periodisch wordt voortgezet.
figuur 5 Sampling van een signaal betekent een eindige selectie van het spectrum beschouwen dat periodisch wordt voortgezet.