Anechoïsche halfruimte

Een anechoïsche halfruimte is een ruimte die (doorgaans onderaan) begrensd wordt door een hard oppervlak, dat de geluidgolven reflecteert. Langs de andere zijden is er in principe geen materiële begrenzing, ofwel worden de geluidgolven volledig geabsorbeerd, en dus niet gereflecteerd.

Realisatie :

binnen in een anechoïsche kamer (ook wel akoestisch dode kamer genoemd) met harde vloer

buiten op bv. een hard betonoppervlak

images/anechoïsche_halfruimte.gif

Types geluid :

alle, behalve impulsachtig geluid (kortstondige, geïsoleerde pieken)

Een internationale norm ter zake bestaat (norm : ISO 3745-1977).

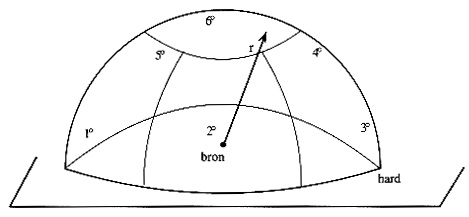	De geluidbron wordt op het hard oppervlak geplaatst.
	De meetpunten, n in aantal, bevinden zich op voldoende afstand van de bron om te waarborgen dat de meting in het vrije, verre geluidveld verricht wordt.
	Verder zijn de n meetpunten zodanig over de halfruimte verdeeld opgesteld (op een half boloppervlak S) dat ieder betrokken is met een gelijk deeloppervlak S_i , dus nS_i = 2pr² .
	De internationale norm geeft de coördinaten van de meetpunten op.

Indien de bron, bv. een machine, niet isotroop afstraalt, meten de diverse microfoons verschillende geluiddrukken. Daarom houden we rekening met een ruimtelijk gemiddelde effectieve geluiddruk p_m in de formule voor het geluidvermogen W = I 2pr² , waarin :

$I=\frac{1}{{\rho}c}\,p_m^2$

We mogen bovenstaande formule gebruiken, want er is een vrij geluidveld boven het hard oppervlak. We gaan nu over op gereduceerde grootheden :

$\frac{W}{W_0}=\frac{p_0^2}{W_0\,{\rho}c}\,\frac{p_m^2}{p_0^2}\,2{\pi}r^2=\frac{p_m^2}{p_0^2}\,2{\pi}r^2$

want voor normale atmosferische omstandigheden (luchtdruk = 10^⁵ Pa , temperatuur = 20 °C) geldt dat :

$\frac{p_0^2}{W_0\,{\rho}c}\approx{1}$

Het geluidvermogenniveau (en daaruit eventueel het geluidvermogen) kan dus bepaald worden met de volgende formule :

$L_W=10\,\log\frac{W}{W_0}=10\,\log\frac{p_m^2}{p_0^2}+10\,\log{r^2}+10\,\log{2{\pi}}$

$L_W=L_{p_m}+20\,\log{r}+8\,\mathrm{dB}\qquad\mathrm{(exact}\,7.98\mathrm{)}$

waarin L_{p_m} op de volgende wijze wordt bepaald :

de n microfoons meten de geluiddrukniveaus L_{p_i} (voor de i-de microfoon, i = 1, 2, ..., n)
$\frac{p_i^2}{p_0^2}=10^{\frac{L_{p_i}}{10}}$
$p_m^2=\frac{1}{S}\,\sum_{i=1}^n\,p_i^2\,S_i\qquad\mathrm{(}=\frac{\sum_{i=1}^n\,p_i^2}{n}\qquad\mathrm{als}\qquad{S_i=}\mathrm{constant)}$
$L_{p_m}=10\,\log\frac{p_m^2}{p_0^2}$

De metingen worden meestal verricht in de genormaliseerde frequentiebanden (1/1 octaafbanden of 1/3 octaafbanden).

auteur : Guy Bladt

not reviewed

gewijzigd op 21/03/00