|
Interne demping in de materialen en structuren zal de geluidoverdracht
verminderen. Bij dit mechanisme wordt beweginsenergie omgezet in warmte. We
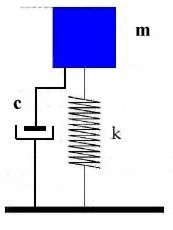
kunnen interne demping behandelen via het eenvoudig model van een enkelvoudige massa-veer
resonator met viskeuze demping waarop een harmonische excitatiekracht inwerkt. |
|
|
|
De grootheden in dit systeem zijn de massa m, de veerconstante k
en de dempingsconstante C. In dit verband wordt gesproken van
dempingsgrootheden zoals kritische demping, half-vermogenbandbreedte, logaritmisch
decrement, enz. Praktisch is het gebruikelijk om te spreken van een interne
dempingsfactor h. Dit is de verhouding tussen de
energie die per bewegingscyclus en per radiaal gedissipeerd wordt, ten opzichte van de
maximale potentiële energie: 
|
|
1. De kinetische en potentiële energie bij een verplaatsing x(t)
= X sin(wt + f)
kunnen we schrijven als volgt:
|
|
%5C%5C%20E_{pot}%5C%20&=&%5C%20%5Cfrac{k}{2}%5C%20x^2%5C%20=%5C%20%5Cfrac{k}{2}%5C%20%5Comega^2%5C%20X^2%5C%20%5Csin^2(%5Comega%20t%5C%20+%5C%20%5Cphi)%5Cend{eqnarray*}%5C%20 "$\begin{eqnarray*}E_{kin}\ &=&\ \frac{m}{2}\ v^2\ =\ \frac{m}{2}\ \omega^2\ X^2\ \cos^2(\omega t\ +\ \phi)\\ E_{pot}\ &=&\ \frac{k}{2}\ x^2\ =\ \frac{k}{2}\ \omega^2\ X^2\ \sin^2(\omega t\ +\ \phi)\end{eqnarray*}$") |
met m: de massa;
w: de
radiale frequentie;
X: het verplaatsingsamplitudo;
x: de verplaatsing;
v: de snelheid dx/dt;
k: de veerconstante. |
|
|
|
|
2. De in 1 cyclus gedissipeerde energie is gelijk aan: 
|
|
De interne demping h
wordt dus gelijk aan:
|
|
De complexe schrijfwijze voor het dynamisch evenwicht bij een harmonische
excitatiekracht F0 ejw t
en in stationaire toestand, levert een ander interessant inzicht in verband met de rol van
de interne dempingsfactor h. %5C%20%5Cunderline%20x%5C%20=%5C%20%5Cunderline%20F_0%5C%20 "$(-\omega^2\ m\ +\ j\omega\ C\ +\ k)\ \underline x\ =\ \underline F_0$")
|
|
met jw x C = C dx/dt
(= de afremkracht door demping) |
|
Het effect van de demping kunnen we nu inrekenen door het gebruik van een
complexe stijfheid k. %5C%20 "$\underline k\ =\ k\ +\ j\omega C\ =\ k(1\ +\ \frac{j\omega C}{k})$")
|
|
Het dynamisch evenwicht kan dus worden vereenvoudigd tot: %5C%20%5Cunderline%20x%5C%20=%5C%20%5Cunderline%20F_0%5C%20 "$(-\omega^2\ m\ +\ \ \underline k)\ \underline x\ =\ \underline F_0$") met %5C%20=%5C%20k(1%5C%20+%5C%20j%5Ceta)%5C%20 "$\underline k\ =\ k(1\ +\ \frac{j\omega C}{k})\ =\ k(1\ +\ j\eta)$") .
|
|
Op dezelfde manier kunnen we stellen dat bij problemen waarbij de
elasticiteitsmodulus een rol speelt, deze vervangen kan worden door een complexe
elasticiteitsmodulus E, die voldoet aan: %5C%20 "$\underline E\ =\ E(1\ +\ j\eta)$") . |
|
|
|
Nu h gedefinieerd is, kunnen we het gedissipeerd vermogen bepalen als |
|
|
(1) |
|
|
waarbij <Epl> de bewegingsenergie is van een
trillende plaat met oppervlakte S. |
|
Indien men dus aan een plaat een vermogen P toevoert, zal deze
een gemiddelde kwadratische snelheid <veff2> krijgen
die gegeven wordt door: |
|
|
(2) |
|
