
|
De periodische sampling van het ingangssignaal leveren ons een
quantitatieve dataset. Het is de bedoeling de karakteristieken van deze dataset
samen te vatten. In eerste instantie wordt nagegaan binnen welke range de waarnemingen
gelegen zijn. Vervolgens wordt de range onderverdeeld in gelijke deelintervallen en wordt
de statistische frequentie van die
verschillende deelintervallen bepaald. |

|
De relatieve statistische frequentie van de
verschillende deelintervallen wordt vervolgens berekend en grafisch weergegeven onder de
vorm van een relatieve statistische frequentie distributie.
|
|
Voorbeeld
Onderstaande tabel toont een dataset van Leq-waarden elke seconde opgemeten.
|

|
Alle waarnemingen zijn gelegen binnen het interval [28.3;
56.1]. We delen dus het interval [28, 58] op in deelintervallen van b.v. 2 dB en bepalen
voor elk deelinterval de statistische frequentie.
|
|
| dB |
Stat. freq. |
| 28 |
9 |
| 30 |
46 |
| 32 |
72 |
| 34 |
54 |
| 36 |
27 |
| 38 |
10 |
| 40 |
12 |
| 42 |
2 |
| 44 |
1 |
| 46 |
2 |
| 48 |
1 |
| 50 |
2 |
| 52 |
1 |
| 54 |
0 |
| 56 |
1 |
| 58 |
0 |
|
Als we deze resultaten grafisch voorstellen, bekomen we de
volgende grafiek: 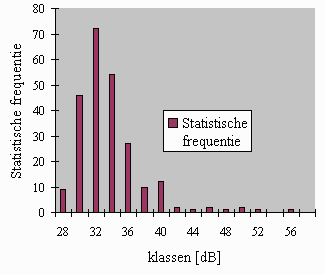
|
|

|
We kunnen nu verder gaan door ook de relatieve
statistische frequentie distributie te bepalen. Daartoe bepalen we voor elk
deelinterval de relatieve statistische frequentie.
|
|
dB |
Stat. freq. |
Relatieve stat. freq. % |
28 |
9 |
3.75% |
30 |
46 |
19.17% |
32 |
72 |
30.00% |
34 |
54 |
22.50% |
36 |
27 |
11.25% |
38 |
10 |
4.17% |
40 |
12 |
5.00% |
42 |
2 |
0.83% |
44 |
1 |
0.42% |
46 |
2 |
0.83% |
48 |
1 |
0.42% |
50 |
2 |
0.83% |
52 |
1 |
0.42% |
54 |
0 |
0.00% |
56 |
1 |
0.42% |
|
Als we dit grafisch voorstellen, krijgen we de volgende
grafiek: 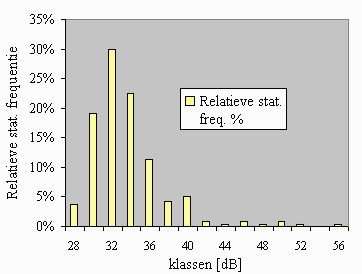
|
Dezelfde informatie kan vervolgens op een andere manier voorgesteld worden. Zo kan
bijvoorbeeld een cumulatieve statistische frequentie distributie getekend worden.
De cumulatieve statistische frequentie behorende bij een bepaald deelinterval is
de som van de relatieve statistische frequenties van het interval in kwestie en van de
voorgaande deelintervallen (gerangschikt van klein naar groot).
Voorbeeld
We werken verder met de gegevens uit vorig voorbeeld. De cumulatieve statistische
frequenties voor de verschillende deelintervallen worden voorgesteld in onderstaande
tabel.
| dB |
Relatieve stat. freq. % |
Cumulatieve stat. freq. % |
| 28 |
3.75% |
3.75% |
| 30 |
19.17% |
22.92% |
| 32 |
30.00% |
52.92% |
| 34 |
22.50% |
75.42% |
| 36 |
11.25% |
86.67% |
| 38 |
4.17% |
90.83% |
| 40 |
5.00% |
95.83% |
| 42 |
0.83% |
96.67% |
| 44 |
0.42% |
97.08% |
| 46 |
0.83% |
97.92% |
| 48 |
0.42% |
98.33% |
| 50 |
0.83% |
99.17% |
| 52 |
0.42% |
99.58% |
| 54 |
0.00% |
99.58% |
| 56 |
0.42% |
100.00% |
|
De cumulatieve statistische frequentie distributie
ziet er dus als volgt uit: 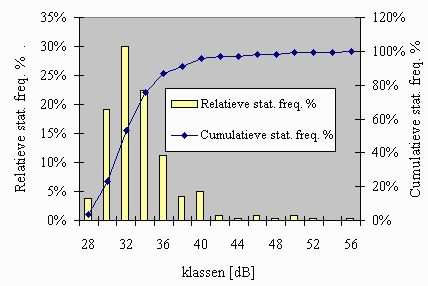
|
De cumulatieve statistische frequentiedistributie is een trapfunctie die kan overgaan
in een continue functie naarmate de deelintervallen verkleind worden. Van dergelijke
cumulatieve statistische frequentie distributies kunnen belangrijke waarden zoals de 5- en
de 95-percentiel direct afgelezen worden.
© INTEC, Universiteit Gent |
