![]()
![]()
![]()
dochters
![]()
level
 de mra-grid
de mra-grid
Wat zijn Wavelets en waarom Wavelets ?
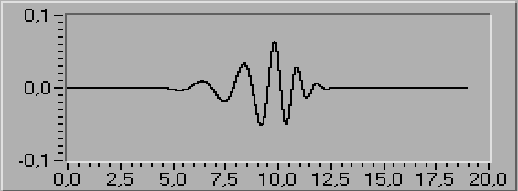
De klassieke Fourieranalyse gebruikt als basissignalen de harmonische signalen .Een grootte van een fouriercoëfficient vertelt ons infeite in welke mate een gegeven signaal lijkt op een bepaalde harmonische componente.
![]()
Vermits echter dit laatste signaal oneindig lang is gaat elke tijdslocatie ,voor het geval het gegeven signaal eindig in duur was, verloren.Het spectrum van een signaal zegt niets over het tijdstip van begin en einde van dit signaal. Short Time Fourier tracht hieraan te verhelpen maar hanteert voor de tijdparameter een constante resolutie zodat zeer korte signalen toch nog niet adequaat geanalyseerd zullen worden.
| Wavelets daarentegen zijn eindige signalen van variabele lengte en bestaan in alle maten en gewichten |

maar met voorts in vele opzichten dezelfde merkwaardige eigenschappen als de harmonische signalen nl zij vormen een volledig stel signalen waarin elk ander signaal kan ontbonden worden en bovendien kunnen zij orthogonaal worden gemaakt zodat invertering van de ontbinding eenvoudig is.Stellen wij de wavelets voor door W(x) dan geldt inderdaad
<W(2n.x-k),W(2m.x-s)> = dn,m.dk,s
de brackets hebben de betekenis van een scalair product net zoals bij de Fourierontwikkelingen.
| Net zoals de harmonische signalen kunnen alle wavelets afgeleid worden uit één moederwavelet door uitrekking en samendrukking. | |
| Een familie van wavelets werd ontwikkeld door een Belgisch wiskundige komende van de VUB nl prof .dr. I.Debauchies, de leden van deze waveletfamilie worden dan ook terecht aangeduid met D2 ,D4, .... D20 (deze laatste werd in bovenliggende figuur afgebeeld). | |
| Net zoals bij Fourier bestaan er snelle afgoritmen F.W.T ( Fast Wavelet Transform) genaamd , uitgewerkt door Mallat en Co die toelaten deze analyse methode praktisch toe te passen soms zelfs in real-time! |
De Basisbetrekkingen
Een signaal f(x) kan ontbonden worden in een reeks van wavelets vertrekkend van de moederwavelet W(x).
![]()
bemerk hierin de gelijkspanningcoëfficient Ao .De coëfficienten Aj,k vormen het waveletspectrum en kunnen in een normaal spectrumdiagramma serieel worden afgebeeld :
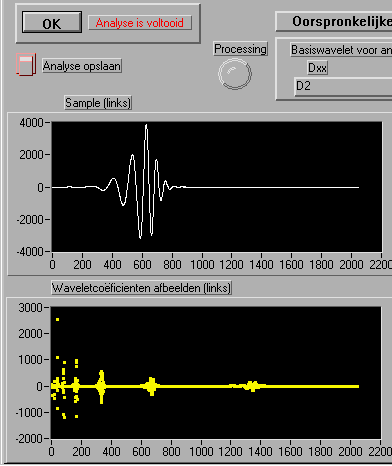 figuur :
het waveletspectrum ééndimensionaal uitgezet
figuur :
het waveletspectrum ééndimensionaal uitgezet
De dochters hiervan worden voorgesteld door
![]()
De parameter k is duidelijk een verschuiving in x over k eenheden dus heeft hij betrekking op een positionering. De parameter j wordt de niveauparameter genaamd ( level-parameter). De betekenis van deze parameter wordt duidelijk als men de functie W(x) , nl de moederwavelet, afbeeldt naast de dochter j=1 nl W(2.x) .Het is overduidelijk dat deze laatste een compressie is met een factor 2 van de moeder. Het spectrum van de dochter ligt dan ook een octaaf hoger dan deze van de moeder vandaar dat de niveauparameter ook overeenkomt met frequentieband .Een verhoging van de niveauparameter j met één eenheid betekent een octaafverhoging.
De waveletcoëfficienten kunnen door de orthogonaliteitseigenschap gemakkelijk gevonden worden :
Aj,k = <f(x),W(2j.x-k)>
maar worden in praktijk berekend met het pyramidiale algoritme van Mallat
De M.R.A ( multi resolutie analyse,vb wavelets ) en zijn grafische voorstelling
You cannot beat the Heisenberg Uncertainty , dus gaat men ze omzeilen door alle tijdsresoluties te gebruiken.Inderdaad zoals wij vroeger gezien hebben bestaat er een verband tussen de tijdsduur van een signaal en de bandbreedte van zijn spectrum.Meestal wordt dit geschreven als
![]()
Voor harmonische signalen is Dt
gelijk aan oneindig zodat de bandbreedte bij de klassieke Fourieranalyse nul is en dus een
zeer goede resolutie vertoont in het spectrum.Bij STFT neemt men echter een vaste
tijdsresolutie ![]() gegeven
door de lengte van een opname T zoals wij weten geeft dit ook een vaste resolutie in
frequentie nl fs/N waar fs de samplingfrequentie is en N het aantal punten in de opname
gegeven
door de lengte van een opname T zoals wij weten geeft dit ook een vaste resolutie in
frequentie nl fs/N waar fs de samplingfrequentie is en N het aantal punten in de opname ![]() .
.
Bij MRA ( vb. de waveletanalyse) neemt men variabele tijdsresoluties. Men begint met
een ![]() gelijk aan de lengte van
een moederwavelet die altijd kan gelijk gemaakt worden met de lengte van de opname.Dan
wordt de moederwavelet gecomprimeerd tot dochters met de halve lengte
gelijk aan de lengte van
een moederwavelet die altijd kan gelijk gemaakt worden met de lengte van de opname.Dan
wordt de moederwavelet gecomprimeerd tot dochters met de halve lengte ![]() /2 ,de bandbreedte van deze dochters
( er zijn er twee want een dochter kan verschoven worden zoals in W(2.x-1) ) is tweemaal
groter dan deze van de moeder. Dan neemt men tweede-generatie dochters
W(4x),W(4x-1),W(4x-2),W(4x-3) , zij behoren tot niveau 2, die elk een bandbreedte hebben
gelijk aan 4-maal deze van de moeder enz....
/2 ,de bandbreedte van deze dochters
( er zijn er twee want een dochter kan verschoven worden zoals in W(2.x-1) ) is tweemaal
groter dan deze van de moeder. Dan neemt men tweede-generatie dochters
W(4x),W(4x-1),W(4x-2),W(4x-3) , zij behoren tot niveau 2, die elk een bandbreedte hebben
gelijk aan 4-maal deze van de moeder enz....
Als men deze opdeling grafisch uitzet in een tijdsas en een niveau-as dan krijgt men het volgende gridpatroon waarin de resoluties , of beter het omgekeerde van dit begrip nl de schalen zowel in tijd als in frequentie duidelijk zijn:
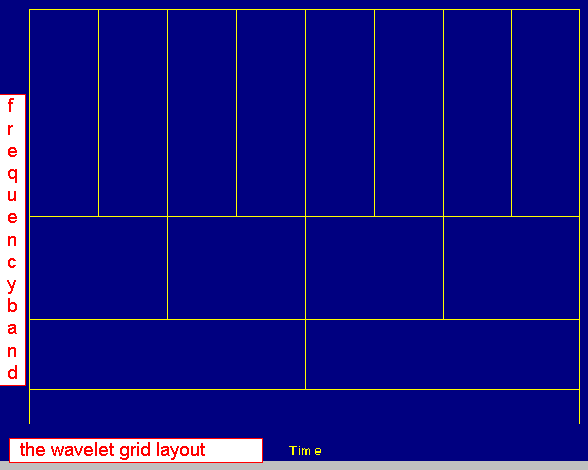
In deze grid gaat men nu de waveletcoëfficienten afbeelden met een kleurcode net zoals in een sonogram. Een voorbeeld ziet u hieronder waar een signaal wordt gebruikt waarin een kras zit. De MRA ontbinding detecteert duidelijk deze kras op de juiste positie , zie onderstaande figuur.
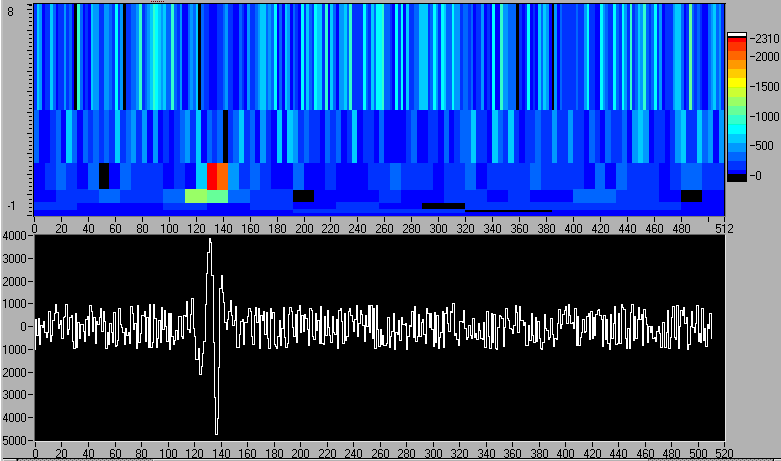
figuur : de kras is duidelijk gelokaliseerd zowel in tijd als in frequentie(band)