Afstraling van eindige platen

In het geval van eindige platen kunnen de formules voor de afstraalfactor zoals ze bepaald zijn in de theorie aangaande afstraling niet zonder meer overgenomen worden. Zo is beneden de grensfrequentie (f < f_gr) de perfecte hydroduynamische kortsluiting niet mogelijk. Er treden nu immers ongecompenseerde rand- of hoekzones op, afhankelijk van de trillingsmode. De afstraalfactor van deze bewegingsvormen is zo altijd groter dan 0.

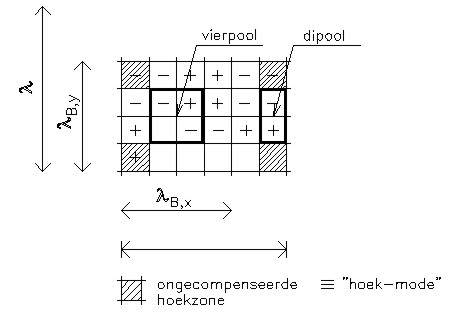
De onderstaande figuur toont een subsonische mode. Dit wil zeggen een mode waarvan de golflengte korter is dan de golflengte van het geluid in de lucht. Deze bewegingsvorm speelt zich dus af in het gebied beneden de grensfrequentie. Wij zien compenserende quadrupolen en dipolen, maar de hoekzones blijven ongecompenseerd over. Men spreekt dan van een 'corner-mode' of derhalve hoekmode. Zo zijn er ook randmodes, waarbij een hele rand ongecompenseerd overblijft.

Bij een puntvormige excitatie is er tevens een ongecompenseerde zone die eveneens de afstraalfactor zal opdrijven.

De demping heeft geen effect op de modevormen, wel op de amplitudo. De afstraalfactor van een modevorm wordt er dus niet door beïnvloed.

Voor twee-dimensionele platen die zwak gedempt zijn en puntsgewijs geëxciteerd worden, geeft men volgende benaderingsformules:

$\begin{eqnarray*} \sigma\ & \approx\ & \frac{U\lambda_{gr}}{\pi^2S}\ \sqrt{\frac{f}{f_{gr}}} \\ \sigma\ & \approx\ & 0,45\ \sqrt{\frac{U}{\lambda_{gr}}} \\ \sigma\ & \approx\ & 1 \end{eqnarray*}$

voor f << f_gr;

voor f = f_gr;

voor f >> f_gr

met

U : de omtreklengte van de plaat
l_gr : de golflengte bij de grensfrequentie
S : de oppervlakte van de plaat