Theorie geluidafstraling

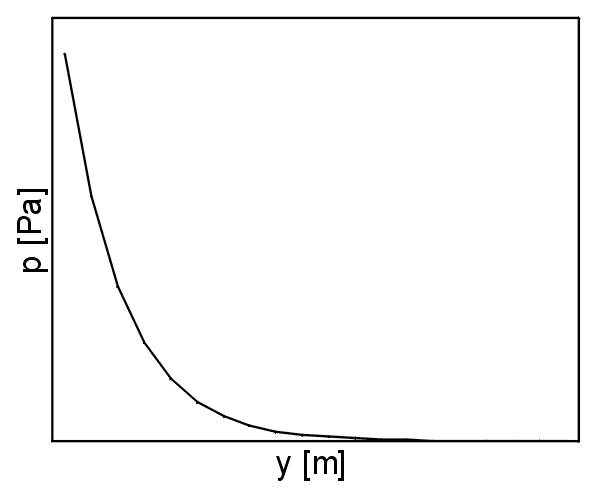
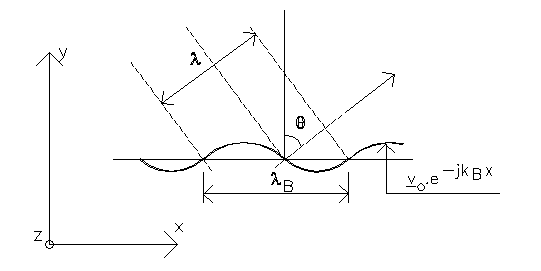
In onderstaande afleiding trachten we te komen tot een berekende waarde voor de afstraalgraad s voor een vlakke harmonische buiggolf. We onderstellen dat deze golf zich voortplant op een oneindig uitgestrekte plaat in de positieve x-richting.

De snelheid van de plaat in de richting loodrecht op de voortplantingsrichting (y-richting in de figuur) varieert met de plaats volgens $\underline v_x\ =\ \underline v_0\ e^{-jk_B\ x}$ .

We wensen nu het geluiddrukveld p(x,y) te berekenen dat ten gevolge van de golfbeweging van de plaat in de omgevende lucht ontstaat. Dit drukveld moet in de x-richting het golfgetal van de buiggolf op de plaat hebben.

p(x,y) kunnen we dus schrijven als: $\underline p(x,y)\ =\ \underline p_0\ e^{-jk_B\ x}\ e^{-jk_y\ y}$ .

(1)

Vergelijkingen

De differentiaalvergelijking van de golfvoortplanting in lucht luidt $\nabla \underline p\ +\ k^2\ \underline p\ =\ 0$

(2)

met als randvoorwaarde in dit geval $\underline v(x,y=0)\ =\ \underline v_0\ e^{-jk_B\ x}$ .

(3)

De vergelijking (2) kunnen we schrijven als (samen met (1)): $-{k^2}_B\ -\ {k^2}_y\ +\ k^2\ =\ 0$ .

De randvoorwaarde (3) wordt: $\underline v(x,y=0)\ =\ \frac{-1}{j\omega\rho}\ \{\frac{\partial\ \underline p}{\partial\ y}\}_{y=0}\ =\ \frac{\underline p_0 k_y}{\omega\rho}\ e^{-jk_B\ x}\ =\ \underline v_0\ e^{-jk_B\ x}$
en dus: $\underline p_0\ =\ \frac{\underline v_0 \omega\rho}{k_y}\ =\ \rho c \underline v_0\ \frac{k}{k_y}$ .

Oplossing

$\underline p(x,y)\ =\ \frac{\underline v_0\ \rho c}{\sqrt{1-\frac{{k^2}_B}{k^2}}}\ e^{-jk_B\ x}\ e^{-j\sqrt{k^2-{k^2}_B}\ y}$ .

In het frequentiedomein bekijken we nu twee gebieden.

beneden de grensfrequentie (f < f_gr)

We kunnen p(x,y) dan schrijven als: $\underline p(x,y)\ =\ \frac{j\underline v_0\ \rho c}{\sqrt{\frac{{k^2}_B}{k^2}-1}}\ e^{-jk_B\ x}\ e^{-\ \sqrt{{k_B}^2-k^2}\ y}$ .
We merken op dat de druk exponentieel afneemt met de afstand tot de wand (zie figuur) volgens $e^^{-\ \sqrt{{k^2}_B-k^2}\ y$ . De andere mathematische mogelijke voorstelling heeft de positieve exponent $e^^{\sqrt{{k^2}_B-k^2}\ y$ . Deze oplossing dienen we echter uit te sluiten op baisis van energetische beschouwingen.

Bepaal nu zelf het afgestraald geluidvermogen en de bijhorende afstraalgraad voor deze situatie. Hoe bewegen de deeltjes in dit geval?

boven de grensfrequentie (f > f_gr)
Het afgestraalde geluidvermogen wordt bepaald uitgaande van:

$\begin{eqnarray*}I\ &=&\ \frac{1}{2}\ \Re\{\frac{\underline{v}_0\ \rho c}{\cos\theta}\ e^{-jk_B\ x}\ \ {\underline{v}_0}^*\ \ e^{+jk_B\ x}\}\\ &\downarrow&\\ I&=&\frac{1}{2}\ {V^2}_0\ \frac{\rho c}{\cos\theta}\end{eqnarray*}$ .
s voldoet dus aan: $\sigma\ =\ \frac{1}{\cos\theta}\ =\ \frac{1}{\sqrt{1-\frac{f_{gr}}{f}}}$ .
Je merkt op dat de afstraalgraad naar oneindig gaat wanneer de hoek q naar 90° gaat. Fysisch is dit onmogelijk. Daarom kunnen we besluiten dat het opgelegde snelheidsveld niet realistisch is. Bovendien hebben we in de realiteit niet te maken met een oneindig uitgestrekte plaat.