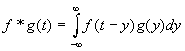1. Intro
Wanneer u in vorig nummer goed hebt toe gekeken dan zoudt u moeten gemerkt hebben dat het spectrum van het oorspronkelijk oneindig lang signaal (nl de dirac-delta's) en het spectrum van het venster ( de lobbenstructuur ) infeite terug te vinden zijn in het volledig spectrum en wel op een zeer eigenaardige manier nl het tweede is gesuperponeerd op het eerste en het oorspronkelijk spectrum wordt hierdoor uitgesmeerd.
2. Convoluties
De wiskundige definitie van deze bewerking is als volgt. Beschouw twee signalen f(t) en g(t) dan is hun convolutie gedefiniëerd als:
Merk op dat één van de twee signalen een translatie in tijd heeft ondergaan. Enkele bijzondere eigenschappen worden hieronder samengevat .
De eerste vergelijking zegt dat de variabelen (t-y) en y mogen van plaats verwisselen in de uitdrukking. De tweede eigenschap verleent zijn naam aan de functie f(t) nl het is de IMPULS RESPONSE van het systeem.Als de functie f(t) causaal zou zijn ,wat wil zeggen dat zij nul is voor alle y > t dan kunnen wij aan deze functie een fysische betekenis geven nl als de invloed die een systeem, bijvoorbeeld een akoestische ruimte of een audiooutput enzomeer, heeft op de meting ergens op een tijdstip t. Maar daarover later meer. Wat is het ogenblikkelijke relevantie van ons nu en hier.
![uitgesmeerd](javascript:popup("images/fourie4.gif");){kind=link}
3. Convolutie en FT, een geslaagd huwelijk
Veronderstel dat men twee signalen heeft of een signaal en een tijdsvenster nl resp. p(t) en v(t) . Van beiden is ook de FT gekend nl Fp(f) en Fv(f) dan geldt
en tevens geldt ook als gevolg van symmetrie tussen tijds-en frequentieruimte:
of
Even verwijlen bij deze belangrijke eigenschappen.
 | De tweede uitdrukking heeft een directe betekenis. Immers een spectrum Fp vermenigvuldigen met een functie Fv wat ook de betekenis van v is is niet min niet meer een filteroperatie in de ruime zin van het woord. En dus kan men ook filteren reeds in het tijdsdomein door het signaal p(t) te convolueren met een filtertijdsfunctie v(t). De zaak is dan deze geschikte filterfunctie te vinden! Maar daarover later (zie Digitale filters). |
| De eerste vermelde eigenschap heeft directe implicaties op een vensteringsoperatie. Neem voor p(t) een harmonisch signaal en beschouw in zijn spectrum één van zijn Dirac Delta spectrale lijn d(f-fo). Venster dit signaal met een venster met lengte Dt .De convolutie van een Dirac Delta functie ( één spectrale lijn) met een venster ( gelijk welk) is dit venster terug .Vermits de Fouriertransformatie van een venster meestal van het type van een gedempte sinus is wil dit zeggen dat elke spectraallijn uitgesmeerd wordt in het spectrum. |