Geluidisolatie dubbele wanden

In veel gevallen is het wenselijk om een hoge geluidisolatie te realiseren met wanden met een laag gewicht. Men kan hier denken aan lichte inbouwwanden, verplaatsbare wanden, vliegtuigconstructies, ...
In dit verband worden dubbele wanden gebruikt. Deze wanden bestaan uit twee spouwbladen met ertussen een luchtlaag of een soepele tussenlaag. Met zulke constructies is het mogelijk een zeer goede geluidisolatie te realiseren met een relatief laag gewicht.

In de veronderstelling dat we een dubbele wand realiseren die bestaat uit twee dezelfde soort platen, met eenzelfde soortelijk gewicht en eenzelfde dikte, hoe denk je dat de geluidisolatie toeneemt?

som van de geluidisolatie van beide afzonderlijke wanden;
gemiddelde van de geluidisolatie van beide afzonderlijke wanden;
geen eenduidig verband.

Het model voor een dubbele wandsysteem is gesteund op het dynamisch evenwicht van twee platen, onderling verbonden door een verend systeem. In de hiernavolgende bespreking volgt een afleiding van de geluidisolatie van dubbele wanden voor loodrechte, schuine en alzijdige inval van een vlakke geluidgolf op de wand.

Bij de bepaling van de vergelijkingen voor de geluidisolatie van dubbele wanden gaan we uit van dezelfde evenwichten als bij de prognosemethode voor enkele wanden. We veronderstellen daarbij dat we te doen hebben met een akoestisch dunne tussenlaag. Dit wil zeggen een tussenlaagdikte d die veel kleiner is dan de golflengte.
Dit levert na vereenvoudigingen twee gebieden op waarbinnen verchillende vergelijkingen geldig zijn.

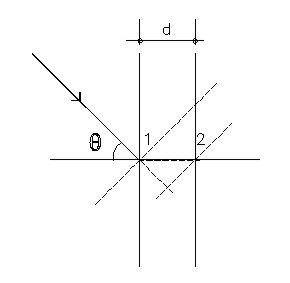
d is de dikte van de spouw [m];
q is de invalshoek van de vlakke golf [°];
m₁^" is de massa van blad 1 [kg/m²];
m₂^" is de massa van blad 2 [kg/m²];

De resonantiefrequentie f₀ voor dit systeem is gegeven door:

$f_0\ =\ \frac{60}{\cos \theta\sqrt{d}}\ \sqrt{\frac{1}{m_1''}\ +\ \frac{1}{m_2''}}$

f Ť f₀(q)

$R\ =\ 20\ \log\frac{\omega\ (m''_1\ +\ m''_2)\ \cos\theta}{2\rho c}$

f ť f₀(q)

$R\ =\ 20\ \log\frac{\omega\ m''_1\ \cos\theta}{2\rho c}\ +\ 20\ \log\frac{\omega\ m''_2\ \cos\theta}{2\rho c}\ +\ 20\ \log\frac{2\omega\ d\ \cos\theta}{c}$

De maximale waarde blijkt omwille van spouwresonanties beperkt tot:

$R\ =\ 20\ \log\frac{\omega\ m''_1\ \cos\theta}{2\rho c}\ +\ 20\ \log\frac{\omega\ m''_2\ \cos\theta}{2\rho c}\ +\ 6$ .
De overgang tussen deze twee laatste formules blijkt voor een invalshoek van 45° gelegen bij $f\ =\ \frac{c}{4d}$ .

Bespreek deze vergelijkingen: hoe verloopt de geluidisolatie in functie van de frequentie en in functie van de invalshoek?

alzijdige inval van een vlakke geluidgolf op een dubbele wand met luchtlaag.

f Ť f0(q)

f ť f0(q)

f Ť f₀(q)

f ť f₀(q)