Actieve geluidcontrole is gebaseerd op het compenseren van lawaai door antigeluid. Voor het beschouwde eendimensionaal probleem kan men het antigeluid opwekken met behulp van één extra geluidbron (= de secundaire geluidbron). Deze luidspreker wordt in de buis aangebracht door een gat te boren in de zijwand (zie figuur).

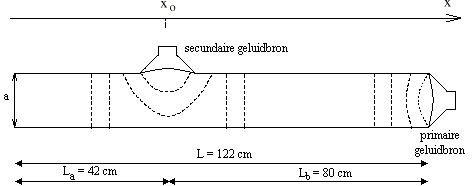
Het geluid dat door deze geluidbron wordt uitgezonden, wekt in de onmiddellijke omgeving van de bron een complex drukpatroon op. Dit drukpatroon kan beschreven worden met de verschillende eigenmodes van de buis. Echter, onder de afsnijfrequentie zullen enkel de nulde-orde modi kunnen propageren door de buis. Men kan de geluidbron dan beschouwen als een vlakke monopoolbron. Deze genereert een naar links en naar rechts propagerende vlakke golf beiden met gelijke amplitude. Voor een oneindig lange buis en in sinusregime worden deze drukgolven beschreven als

p(x) = p_s e ^{-ik |x-x0|}

waarbij x_o de positie van de luidspreker weergeeft, k het golfgetal en p_s de door de secundaire bron gegenereerde amplitude. De verliezen in de buis worden verwaarloosd.

Bij combinatie met het geluid van de primaire bron en rekening houdend met een zekere reflectie van het geluid van de secundaire bron aan de primaire bron bekomt men de situatie geschetst in onderstaande figuur.

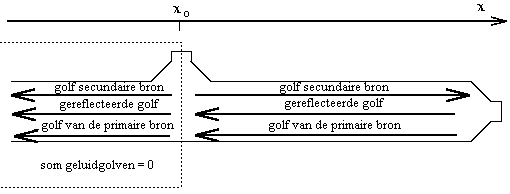
Voorbij de secundaire bron in de richting van de uitgang bekomt men (x < x_o)

p_tot  =  0  =  p_s e ^{ik (x-xo)}  +  R p_s e^{ik (x-xo - 2Lb)}  +  p_p e ^{ik (x-xo - Lb)}

met:

de constante R de drukreflectiecoëfficiënt aan de primaire bron (voor de eenvoud wordt R reëel beschouwd)
p_p is de amplitude die wordt gegenereerd door de primaire bron ter hoogte van de bron
L_b is de afstand van de primaire bron tot de secundaire luidspreker.

Door p_s gelijkt te kiezen aan

kan men de totale druk nul krijgen en dit voor alle x < x_o.

Bemerk dat de gewenste secundaire druk evenredig is met de primaire (originele) druk, maar dat deze met een frequentieafhankelijke complexe factor vermenigvuldigd wordt.