afleiding LMS-algoritme

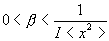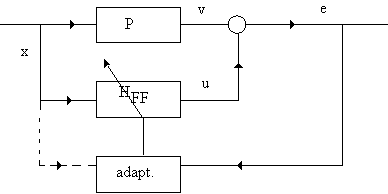
Het LMS-algoritme vormt de basis voor vele adaptieve digitale systemen. Het algoritme past de coëfficiënten van een digitaal FIR filter aan tot het verschil e tussen de output u van het filter en een gewenst signaal v nul wordt. Het FIR filter heeft een transfertfunctie beschreven door

$u_n = H_{FF}(x)= \sum_j a_j\,x_{n-j}$

waarbij de index de digitale tijdsafhankelijkheid aanduidt. De coëfficiënten a_j moeten nu bepaald worden zodat het foutsignaal e minimaal wordt. Numeriek wordt dit beschreven door te eisen dat de verwachtingswaarde van de kwadratische fout,<e²>, minimaal wordt. De <> verwijst naar een tijdsmiddeling over een voldoende lang tijdsinterval. Voor <e²> bekomen we:

$\left\langle e^2 \right\rangle = \frac{1}{N}\sum_n \sum_{i,j}a_j\,a_i\,x_{n-j}\,x_{n-i} + \frac{2}{N}\sum_{n}\sum_{j}a_jx_{n-j}v_n + \frac{1}{N}\sum_n \rm{v}_n$

waarbij over N tijdstappen werd uitgemiddeld. Dit is een kwadratische functie in de a_j. Een uniek minimum is dan ook gegarandeerd. Het minimum kan gevonden worden door de afgeleide naar elk van de a_j nul te stellen. De afgeleide is:

$\matrix{ {\frac{\partial \langle e^2 \rangle}{\partial a_j}} \hfill & {=\frac{2}{N}\,\sum_n\sum_ia_i\, x_{n-i}\, x_{n-j} + \frac{2}{N}\,x_{n-j}\rm{v}_n} \hfill \cr {} \hfill & {=\frac{2}{N}\,\sum_n\,x_{n-j}\,e_n } \hfill \cr }$

Dit geeft ons een stelsel in de onbekende filtercoëfficiënten dat perfect op te lossen is. Het minimaliseren kan echter ook gebeuren door de aj iteratief aan te passen, rekening houdend met de afgeleide van <e²> naar a_j. In optimalisatietheorie wordt dit de steepest descent methode genoemd. Bij elke iteratie wordt bij de respectievelijke coëfficiënten een fractie van de overeenkomstige afgeleide opgeteld. Zo stapt men steeds in de richting van de lagere <e2> tot het minimum bereikt is en de afgeleiden nul worden. De gemiddelde waarde berekenen is numeriek een zeer tijdrovende aangelegenheid. Zeker wanneer het gewenste signaal v verandert in de tijd is het noodzakelijk voldoende snel de filtercoëfficiënten te kunnen aanpassen. Het LMS-algoritme brengt de oplossing. Het LMS-algoritme bestaat erin enerzijds de tijdsmiddeling (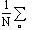) te verwaarlozen, anderzijds de correctie op de coëfficiënten te vermenigvuldigen met een stabilisatiefactor b. Het resultaat is een iteratieve correctie op de filtercoëfficiënten aj van de vorm:

$a_j^{n+1}= a_j^n + \beta.x_{n-j}.e_n \,\,\,\, \forall j$

waarbij de bovenindex naar de iteratiestap verwijst. Dit is natuurlijk een zeer drastische benadering. Formeel bewijzen dat het LMS-algoritme convergeert naar de minimale fout is enkel haalbaar bij extreme signalen zoals zuivere sinus of witte ruis. Nochtans leert de praktijk dat ook voor willekeurige signalen de convergentie-eigenschappen goed zijn indien men b goed kiest. Een vuistregel voor de keuze van b is:

met I het aantal filtercoëfficiënten en <x²> de verwachtingswaarde van het referentiesignaal.

<<experimenteerikoontje met link naar applet op het net>>

gewijzigd op 31/05/00

auteurs : Dick Botteldooren, Pieter Vandaele

reviewer : Raoul Meuldermans