wanden met buigstijfheid

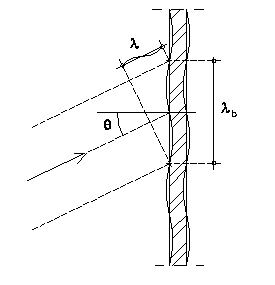
We veronderstellen vlakke golven die invallen op een wand met buigstijfheid. Door de dynamische vervorming ontstaat op de plaat een buiggolf.

l = golflengte van de invallende golf.
l_b = golflengte van de buiggolf op de plaat.
q = invalshoek van de geluidgolf.

1. Schuine vlakke golf invallend op een wand met buigstijfheid

Weerom kunnen we uit het dynamisch evenwicht de geluidisolatie afleiden.
$R =10\cdot \log\{1+\{ \frac{\omega m'' \cos\theta}{2Z}\cdot[1-(\frac{c_B\sin\theta}{c})^4]\}^2\}$

De weerstand van de muur valt weg wanneer $c_B =\frac{c}{\sin \theta}$ . Geometrisch betekent dit dat het 'spoor' van de invallende golf op de plaat zich voortplant met de voortplantingssnelheid van een zich vrij voortplantende buiggolf bij dezelfde frequentie. Dit fenomeen noemt men coïncidentie of spooraanpassing. De laagste frequentie waarbij het fenomeen zich kan voordoen, noemt men de grensfrequentie. Dan is c = c_B.

In combinatie met de uitdrukking voor de voortplantingssnelheid van de buiggolf op de plaat c_B, berekent men de grensfrequentie dan als: $f_{gr} = \frac{c^2}{2\pi}\sqrt{\frac{m'}{B}}$ .
B is de buigstijfheid voor de eenheidsbreedte van 1 m en is gelijk aan: $B\ =\ \frac{E\ I}{(1\ -\ \mu^2)}$ . I is het traagheidsmoment en is voor de eenheidsbreedte gelijk aan: $I\ =\ \frac{1\cdot h^3}{12}$ . m' is het gewicht per lengte-eenheid.

Het product van de grensfrequentie met de dikte van de wand blijkt na vereenvoudiging enkel af te hangen van de materiaalconstanten r_p, E en m. Het kan als volgt geschreven worden:

$f_{gr} h \approx \frac{64000}{c_L}$

c_L is de quasi-longitudinale golfsnelheid in de plaat: $c_L = \sqrt {\frac{E}{\rho_p(1-\mu^2)}$ .

De geluidisolatie blijkt sterk afhankelijk te zijn van de invalshoek. Bij scherende inval is de geluidisolatie zelfs gelijk aan 0.

2. Alzijdig invallende vlakke golf op een wand met demping en buigstijfheid

De invloed van de interne demping wordt vervat in een complexe elasticiteitsmodulus E = E(1+jh).
We kunnen aldus berekenen dat de geluidisolatie voor een golf die onder een hoek q invalt op de wand, gelijk wordt aan:

$R = 10\cdot \log \{ [{\frac{\omega m'' \cos\theta}{2\rho c}(1-\big[\frac{c_B \sin\theta}{c}\big]^4)]^2+[1+\eta\frac{\omega m''\cos\theta}{2\rho c}\big[\frac{c_B\sin\theta}{c}\big]^4]^2\}$ .

Voor het gebied boven de grensfrequentie kan men, na integratie over de invalshoeken 0° tot 80 °, benaderend de volgende formule voor de alzijdige geluidisolatie aannemen (voor h > 0,04 en f > 2 f_gr):

$R_{alz} \approx R_0(f_{gr}) + 10\cdot\log\eta + 30\cdot\log\frac{f}{f_{gr}} -2$

Hoe ziet het geluidisolatieverloop eruit? Analyseer hierbij de verschillende parameters.

Volg deze link voor enkele demo's van de deeltjesbeweging van een golf die invalt onder een bepaalde hoek op een oneindig uitgestrekte wand. Een deel van de golf wordt gereflecteerd door de wand. Een ander deel gaat door de wand heen.

Praktische methode

De prognosemethode is een benaderende methode voor het bepalen van de geluidisolatie.