
|
probleemstelling:
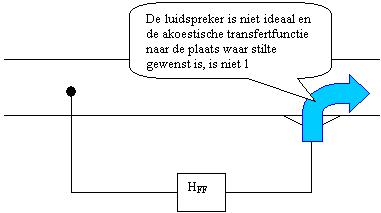
De elektroakoestische componenten, die in het aktief controlesysteem gebruikt
worden, zijn geen ideale elementen. Bovendien is de transfertfunctie tussen het geluid van
de secundaire bron en de foutmicrofoon niet 1. Schematisch voorgesteld geeft dit:
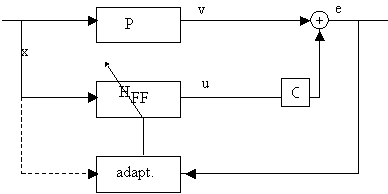
De transfertfunctie C vervormt het uitgangssignaal van HFF zodanig dat <e2>
geen kwadratische functie meer is van de filtercoŽfficiŽnten. Aangezien de werking van
het LMS algoritme op deze eigenschap steunt, is de convergentie niet meer gegarandeerd.
We moeten er dus voor zorgen dat u rechtstreeks in het foutsignaal e terecht komt.
Theoretisch is dit eenvoudig realiseerbaar: voor de secundaire bron plaatsen we een
bijkomend filter dat precies het inverse van C is, nl. C-1. Hoe dit filter
bekomen wordt, bespreken we verder. Eerst worden enkele varianten op de plaats van het
bijkomend filter bekeken. |
|
 | Filtered u
|
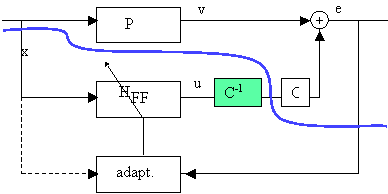
Dit is de vorm, die men dadelijk bekomt. Voor de duidelijkheid is de grens tussen
elektro-akoestisch gedeelte en digitaal gedeelte met een blauwe lijn aangeduid. De
herkomst van de naam is duidelijk: het uitgangssignaal u wordt gefilterd. Het nadeel van
deze vorm is dat een extra filter (i.e. extra filtercoŽfficiŽnten) in het voorwaardse
pad worden bijgevoegd. Alle berekeningen die in dit pad gebeuren moeten voldoende snel
zijn zodat het secundaire signaal op tijd berekent is. Door het toevoegen van het extra
filter kan het nodig worden om het referentiesignaal vroeger (meer naar links in de
hierboven getekende buis) op te pikken zodat er meer tijd is voor de berekening.
 | Filtered-x
|
We schuiven nu het bijkomend filter op naar links. Alhoewel HFF in de tijd
verandert en dus strikt genomen de volgorde van de filters niet mag omgewisseld worden
(geen lineair tijdsinvariante systemen), zal de verandering traag zijn en wordt de
volgordewissel toch getollereerd. Vervolgens verschuiven we het filter tot voorbij de
splitsing van x over HFF-filter en LMS-algoritme. Hierbij moet een bijkomend
filter C ingevoerd worden zodat het signaal naar het LMS behouden blijft. Tot slot
argumenteren we dat het referentiesignaal x enkel goed gecorreleerd moet zijn met v, maar
voor de rest rustig vervormd mag worden, zodat het filter C-1 kan weggelaten
worden. Dit geeft ons het schema voor een filtered-x oplossing. De keuze van de naam is
duidelijk. Het filtered-x algoritme blijkt snel te convergeren en eerder robuust te zijn
voor fouten in de schatting van het digitale filter C.
 | Filtered-e
|
Een laatste variant wordt bekomen door het bijkomend digitaal filter naar rechts door
te schuiven. Volgorde wissel met C is geen probleem. Een virtueel filter C moet toegevoegd
worden in het akoestisch pad P zodat de bijdrage van v tot de fout onveranderd blijft. In
de zin dat P niet te snel verandert in de tijd kan opnieuw een wissel gebeuren. Tenslotte
kunnen we opnieuw argumenteren voor het weglaten van het virtueel filteren van x voor P
wegens het feit dat enkel een goed gecorreleerd referentiesignaal nodig is. Het bekomen
schema wordt filtered-e genoemd en is veel minder populair. Een van de redenen hiervoor is
dat nu niet meer het foutsignaal, maar een gefilterde versie ervan geminimaliseerd wordt.
In sommige gevallen kan dit aanleiding geven tot een overblijvend geluid e dat ongewenste
spectrale pieken bevat.
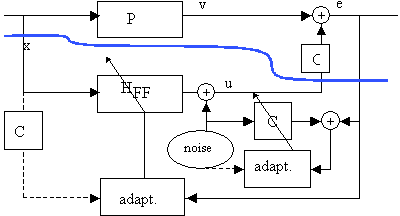
We moeten nu nog het filter C, respectievelijk C-1 bepalen. Net zoals bij
het hoofd-pad P, kan de transfertfunctie tussen u en e veranderen in de tijd. Een
adaptieve bepaling van C is dus gewenst. Dit gebeurt door bijkomende ruis (ongecorreleerd
met x) naar de secundaire bron te sturen. De ruis wordt eveneens door een FIR filter C
gestuurd. Het resultaat wordt afgetrokken van e en dit signaal wordt gebruikt als
foutsignaal in een tweede LMS adaptief algoritme dat C aanpast. Nu en dan worden de
filtercoŽfficiŽnten gekopieerd naar het filter in het primaire pad. Hieronder is het
schema gegeven voor het aangepaste filtered-x algoritme.
|
© INTEC, Universiteit Gent
|
